EM-103 | Shear Force & Bending Moment Apparatus

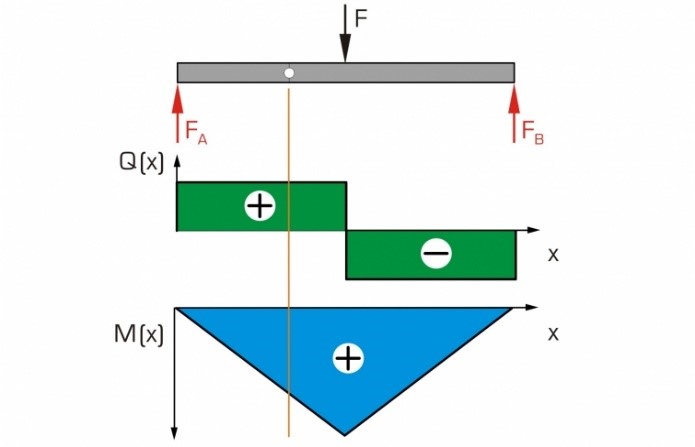
Statics observes the effect of forces on a rigid body, ignoring any possible deformations which may occur in the process. The forces are in equilibrium. A simple example is a statically determinate bearing-mounted beam subjected to point loads. The reactions are determined from the conditions of equilibrium. To investigate the effect of the point loads in the beam, it is notionally split into two segments. Applying the method of sections, the internal forces and moments are plotted onto the two segments and calculated by way of conditions of equilibrium. It includes a beam mounted on two supports. The beam is cut at one point. At that point there is a low-friction hinge with two degrees of freedom. Two force gauges determine the internal reactions to the externally applied forces at the section. The shear force is recorded and displayed directly by a force gauge. The bending moment occurring at the section is recorded by a second force gauge acting on a fixed lever arm. Adjuster nuts on the two force gauges are used to align the beam horizontally and balance out any deflection. In evaluating the experiment, it becomes clear that the shear force, as opposed to the bending moment, is mostly negligible when designing components.

Learning Objectives

• Calculation of the reactions arising from the static conditions of equilibrium
• Application of the method of sections to calculate the internal forces and moments
• Under a point load
• Under multiple point loads
• Calculation of the shear force diagram
• Calculation of the bending moment diagram
• Comparison of calculated and measured values for shear force and bending moment